Exponents are shorthand for repeated multiplication of the same thing by itself. For instance, the shorthand for multiplying three copies of the number 5 is shown on the right-hand side of the "equals" sign in (5)(5)(5) = 53. The "exponent", being 3 in this example, stands for however many times the value is being multiplied. The thing that's being multiplied, being 5 in this example, is called the "base".
This process of using exponents is called "raising to a power", where the exponent is the "power". The expression "53" is pronounced as "five, raised to the third power" or "five to the third". There are two specially-named powers: "to the second power" is generally pronounced as "squared", and "to the third power" is generally pronounced as "cubed". So "53" is commonly pronounced as "five cubed".
When we deal with numbers, we usually just simplify; we'd rather deal with "27" than with "33". But with variables, we need the exponents, because we'd rather deal with "x6" than with "xxxxxx".
Exponents have a few rules that we can use for simplifying expressions.
For instance, given (3 + 4)2, do NOT succumb to the temptation to say "This equals 32 + 42 = 9 + 16 = 25", because this is wrong. Actually, (3 + 4)2 = (7)2 = 49, not 25. When in doubt, write out the expression according to the definition of the power. Given (x – 2)2, don't try to do this in your head. Instead, write it out: "squared" means "times itself", so (x – 2)2 = (x – 2)(x – 2) = xx – 2x – 2x + 4 = x2 – 4x + 4.
The mistake of erroneously trying to "distribute" the exponent is most often made when the student is trying to do everything in his head, instead of showing his work. Do things neatly, and you won't be as likely to make this mistake.
There is one other rule that may or may not be covered at this stage:
This process of using exponents is called "raising to a power", where the exponent is the "power". The expression "53" is pronounced as "five, raised to the third power" or "five to the third". There are two specially-named powers: "to the second power" is generally pronounced as "squared", and "to the third power" is generally pronounced as "cubed". So "53" is commonly pronounced as "five cubed".
When we deal with numbers, we usually just simplify; we'd rather deal with "27" than with "33". But with variables, we need the exponents, because we'd rather deal with "x6" than with "xxxxxx".
Exponents have a few rules that we can use for simplifying expressions.
- Simplify (x3)(x4) Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved
- To simplify this, I can think in terms of what those exponents mean. "To the third" means "multiplying three copies" and "to the fourth" means "multiplying four copies". Using this fact, I can "expand" the two factors, and then work backwards to the simplified form:
- (x3)(x4) = (xxx)(xxxx)
= xxxxxxx
= x7
( x m ) ( x n ) = x( m + n )
- Simplify (x2)4
- Just as with the previous exercise, I can think in terms of what the exponents mean. The "to the fourth" means that I'm multiplying four copies of x2:
- (x2)4 = (x2)(x2)(x2)(x2)
= (xx)(xx)(xx)(xx)
= xxxxxxxx
= x8
- ( xm ) n = x m n
For instance, given (3 + 4)2, do NOT succumb to the temptation to say "This equals 32 + 42 = 9 + 16 = 25", because this is wrong. Actually, (3 + 4)2 = (7)2 = 49, not 25. When in doubt, write out the expression according to the definition of the power. Given (x – 2)2, don't try to do this in your head. Instead, write it out: "squared" means "times itself", so (x – 2)2 = (x – 2)(x – 2) = xx – 2x – 2x + 4 = x2 – 4x + 4.
The mistake of erroneously trying to "distribute" the exponent is most often made when the student is trying to do everything in his head, instead of showing his work. Do things neatly, and you won't be as likely to make this mistake.
There is one other rule that may or may not be covered at this stage:
- Anything to the power zero is just "1".
- Simplify [(3x4y7z12)5 (–5x9y3z4)2]0 Who cares about that stuff inside the square brackets? I don't, because the zero power on the outside means that the value of the entire thing is just 1.
- --------------------------------------------------------------------------
- A negative exponent just means that the base is on the wrong side of the fraction line, so you need to flip the base to the other side. For instance, "x–2" (ecks to the minus two) just means "x2, but underneath, as in 1/(x2)".
- Write x–4 using only positive exponents.
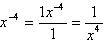
- Write x2 / x–3 using only positive exponents.
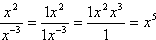
- Write 2x–1 using only positive exponents.
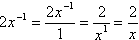
- Write (3x)–2 using only positive exponents.
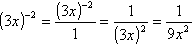
- Write (x–2 / y–3)–2 using only positive exponents.
![[ x^(-2) / y^(-3) ]^(-2) = [ y^(-3) / x^(-2) ]^2 = [ y^(-6) ] / [ x^(-4) ] = (x^4)/(y^6)](http://www.purplemath.com/modules/exponent/exp06.gif)
![[ x^(×2) / y^(-3) ]^(-2) = [ x^(-2) ]^-2 / [ y^(-3) ]^(-2) = (x^4) / (y^6)](http://www.purplemath.com/modules/exponent/exp07.gif)
By the way, now that you know about negative exponents, you can understand the logic behind the "anything to the power zero" rule:
- Anything to the power zero is just "1".
- 35 = 36 ÷ 3 = 36 ÷ 31 = 36–1 = 35= 243
34 = 35 ÷ 3 = 35 ÷ 31 = 35–1 = 34= 81
33 = 34 ÷ 3 = 34 ÷ 31 = 34–1 = 33= 27
32 = 33 ÷ 3 = 33 ÷ 31 = 33–1 = 32= 9
31 = 32 ÷ 3 = 32 ÷ 31 = 32–1 = 31= 3
A negative-exponents explanation of the "anything to the zero power is just 1" might be as follows:
- m0 = m(n – n) = mn × m–n = mn ÷ mn = 1
Another comment: Please don't ask me to "define" 00. There are at least two ways of looking at this quantity:
- Anything to the zero power is "1", so 00 = 1.
- Zero to any power is zero, so 00 = 0.
- Write x–4 using only positive exponents.
- ------------------------------------------------------- By using exponents, we can reformat numbers. For very large or very small numbers, it is sometimes simpler to use "scientific notation" (so called, because scientists often deal with very large and very small numbers). The format for writing a number in scientific notation is fairly simple: (first digit of the number) followed by (the decimal point) and then (all the rest of the digits of the number), times (10 to an appropriate power). The conversion is fairly simple.
- Write 124 in scientific notation.
- Write in decimal notation: 3.6 × 1012
- Write 0.000 000 000 043 6 in scientific notation.
- Convert 4.2 × 10–7 to decimal notation.
- Convert 0.000 000 005 78 to scientific notation.
- Convert 93,000,000 to scientific notation.
- Simplify and express in scientific notation: (2.6 × 105) (9.2 × 10–13)
- Simplify and express in scientific notation: (1.247 × 10–3) ÷ (2.9 × 10–2)
- -------------------------------
- "Engineering" notation is very similar to scientific notation, except that the power on ten can only be a multiple of three. In this way, numbers are always stated in terms of thousands, millions, billions, etc. For instance, 13,460,972 is thirteen million and some. In the newspaper, it would probably be abbreviated as "13.5 million". In engineering notation, you would move the decimal point six places to the left to get 13.460972 × 106. Once you get used to this notation, you recognize that 106 means "millions", so you would see right away that this is around 13.5 million. Every time a newspaper refers to some number of millions or billions or trillions, rather than writing out the whole number with all the zeroes, it is, in effect, using engineering notation.
- Express 472,690,128,340 in engineering notation.
- This is a twelve-digit number. I need to move the decimal point from the end of the number toward the beginning of the number, but I must move it in steps of three decimal places. In this case, I must move the decimal point to between the 2 and the 6, because this will leave nine digits (and nine is a multiple of 3) after the decimal point, and no more than three digits before the decimal point. Then the answer is:
- 472.690128340 × 109, or 472.7 billions.
- Express 83,201 in engineering notation.
- I need to move the decimal point over to the left in sets of three digits. I can't move the decimal point any further than to the left of the 2, which is three places, so the answer is:
- 83.201 × 103, or 83.201 thousands.
- Express 0.000 063 8 in engineering notation.
- I need to move the decimal point over in sets of three. If I move the decimal point to the right three places, I'll be left with "0.0638", which won't do. If I move the decimal point to the right nine places, I'll get "63800", which is too many digits. So I need to move the decimal point six places. Since this started out as a small number, the power on 10 will be negative, and the answer is: Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved
- 63.8 × 10–6, or 63.8 millionths.
- Express 0.397 53 in engineering notation.
- I need to move the decimal point to the right three places. Since this started as a small number, the power on 10 will be negative:
- 397.53 × 10–3, or 397.53 thousandths.
- --------------------------------------------------------------------------
- You already know of one relationship between exponents and radicals: the appropriate radical will "undo" an exponent, and the right power will "undo" a root. For example:

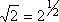
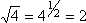
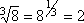
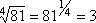
Looking at the first examples, we can re-write them like this:
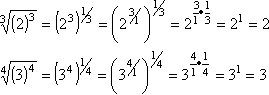
Fractional exponents allow greater flexibility (you'll see this a lot in calculus), are often easier to write than the equivalent radical format, and permit you to do calculations that you couldn't before. For instance:
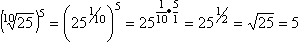
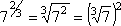
- 35.5 = 311/2
A technical point: When you are dealing with these exponents with variables, you might have to take account of the fact that you are sometimes taking even roots. Think about it: Suppose you start with the number –2. Then:
![sqrt[ (-2)^2 ] = sqrt(4) = 2, does not equal -2](http://www.purplemath.com/modules/exponent/exp23.gif)
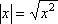
A technology point: Calculators and other software do not compute things the way people do; they use pre-programmed algorithms. Sometimes the particular method the calculator uses can create difficulties in the context of fractional exponents.
For instance, you know that the cube root of –8 is –2, and the square of –2 is 4, so (–8)(2/3) = 4. But some calculators return a complex value or an error message, as is the case with one of my graphing calculators: 
If you enter "=(–8)^(2/3)" into a cell, the Microsoft "Excel" spreadsheet returns the error "#NUM!".
Some calculators and programs will do the computations as expected, as displayed at right from my other graphing calculator:
The difference has to do with the pre-programmed calculating algorithms. These algorithms generally try to do the computations in ways which require the fewest "operations", in order to process what you've entered as quickly as possible. But sometimes the fastest method isn't always the most useful, and your calculator will "choke".
Fortunately, you can get around the problem: by splitting the numerator and denominator of the fractional power, your calculator should arrive at the correct value:
As you can see above, it didn't matter if I first took the cube root of negative eight and then squared, or if I first squared and then cube-rooted; either way, the calculator returned the proper value of "4"
الطالبات:
وجدان محمد العتيبي
لمى عبدالعزيز القصير
R6.
- This is not a very large number, but it will work nicely for an example. To convert this to scientific notation, I first write "1.24". This is not the same number, but (1.24)(100) = 124 is, and 100 = 102. Then, in scientific notation, 124 is written as 1.24 × 102.
- Since the exponent on 10 is positive, I know they are looking for a LARGE number, so I'll need to move the decimal point to the right, in order to make the number LARGER. Since the exponent on 10 is "12", I'll need to move the decimal point twelve places over. First, I'll move the decimal point twelve places over. I make little loops when I count off the places, to keep track:
- In scientific notation, the number part (as opposed to the ten-to-a-power part) will be "4.36". So I will count how many places the decimal point has to move to get from where it is now to where it needs to be:
- Since the exponent on 10 is negative, I am looking for a small number. Since the exponent is a seven, I will be moving the decimal point seven places. Since I need to move the point to get a small number, I'll be moving it to the left. The answer is 0.000 000 42
- This is a small number, so the exponent on 10 will be negative. The first "interesting" digit in this number is the 5, so that's where the decimal point will need to go. To get from where it is to right after the 5, the decimal point will need to move nine places to the right. Then the power on 10 will be a negative 9, and the answer is 5.78 × 10–9
- This is a large number, so the exponent on 10 will be positive. The first "interesting" digit in this number is the leading 9, so that's where the decimal point will need to go. To get from where it is to right after the 9, the decimal point will need to move seven places to the left. Then the power on 10 will be a positive 7, and the answer is 9.3 × 107
- –0.00036 = –3.6 × 10–4 0.00036 = 3.6 × 10–4 36,000 = 3.6 × 104 –36,000 = –3.6 × 104
You might be asked to multiply and divide numbers in scientific notation. I've never really seen the point of this, since, in "real life", you'd be dealing with these messy numbers by using a calculator, but here's the process.
- Since I'm multiplying, I can move things around and simplify some of this stuff easily:
- (2.6 × 105) (9.2 × 10–13) = (2.6)(105)(9.2)(10–13) = (2.6)(9.2)(105)(10–13) = (2.6)(9.2)(105–13) = (2.6)(9.2)(10–8)
- 2.6 × 9.2 = 23.92 = 2.392 × 10 = 2.392 × 101
- (2.6 × 105) (9.2 × 10–13) = (2.6)(9.2)(10–8) = (2.392 × 101)(10–8) = (2.392)(101)(10–8) = (2.392)(101–8) = 2.392 × 10–7
- First, I'll deal with the exponents:
- (1.247 × 10–3) ÷ (2.9 × 10–2) = (1.247 ÷ 2.9) (10–3 ÷ 10–2) = (1.247 ÷ 2.9) (10–3 × 102) = (1.247 ÷ 2.9) (10–1)
- 1.247 ÷ 2.9 = 0.43 = 4.3 × 10–1
- (1.247 × 10–3) ÷ (2.9 × 10–2) = (1.247 ÷ 2.9) (10–1) = (4.3 × 10–1) (10–1) = (4.3)(10–1)(10–1) = (4.3)(10–2) = 4.3 × 10–2
If you're looking to lose kilograms then you certainly need to get on this totally brand new custom keto meal plan diet.
ردحذفTo create this service, certified nutritionists, fitness couches, and professional chefs have joined together to produce keto meal plans that are productive, convenient, cost-efficient, and enjoyable.
Since their grand opening in 2019, thousands of individuals have already completely transformed their figure and well-being with the benefits a professional keto meal plan diet can provide.
Speaking of benefits: clicking this link, you'll discover eight scientifically-proven ones offered by the keto meal plan diet.
Strange "water hack" burns 2 lbs in your sleep
ردحذفMore than 160k men and women are utilizing a easy and SECRET "water hack" to burn 1-2 lbs every night while they sleep.
It's proven and works on everybody.
Here's how you can do it yourself:
1) Grab a clear glass and fill it up half glass
2) Proceed to learn this awesome HACK
and be 1-2 lbs skinnier the next day!